Injektionssysteme für Dübel haben in den vergangenen Jahren immer mehr an Bedeutung gewonnen. Leistungsfähige Injektionsmörtel eignen sich auf Grund ihrer hohen Verbundfestigkeit zur Verankerung von Gewindestangen und Innengewindehülsen aber auch von Bewehrungsstäben. Dabei unterscheidet man Bewehrungsstäbe, die als Dübel verwendet werden, und Stäbe für nachträgliche Bewehrungsanschlüsse. Entsprechend unterschiedlich sind die Bemessungsverfahren.

Werden Bewehrungsstäbe als Dübel verwendet, dann werden sie auf Basis von ETAG 001, Technical Report TR 029 bemessen (Dübeltheorie). Sie können durch Zug- und Querlasten beansprucht werden und versagen wie chemische Dübel.

Werden Bewehrungsstäbe für nachträgliche Bewehrungsanschlüsse verwendet, dann gelten die Regeln des Stahlbetonbaus und die Bemessung erfolgt nach Eurocode 2 (EN 1992-1-1:2004: Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken – Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau). In diesen Fällen dürfen die Stäbe nur durch Zuglasten beansprucht werden und als Versagensart kann Stahlbruch, Herausziehen oder Spalten auftreten.

Während einbetonierte Bewehrungsstäbe Zuglasten über die Bewehrungsrippen direkt in den umgebenden Beton einleiten, werden Lasten bei eingemörtelten Bewehrungsstäben zunächst über die Rippen in den ausgehärteten Injektionsmörtel und von dort über Mikroverzahnung und Klebewirkung in den Beton weitergeleitet. Bei geeigneten zugelassenen Injektionssystemen tritt der Bruch - wie bei einbetonierten Bewehrungsstäben - in der Fuge zwischen Rippen und Injektionsmörtel auf.

Bewehrungsstäbe können ohne oder mit Anschlussbewehrung eingemörtelt werden. Im ersten Fall spricht man von Verankerungen, im zweiten von Übergreifungsstößen. Bild 1 zeigt den Verlauf der Zugspannungen einer Verankerung (Spieth, A. H.: Tragverhalten und Bemessung von eingemörtelten Bewehrungsstäben. Dissertation. Universität Stuttgart, 2002). Bei Übergreifungsstößen wird eine Zugkraft im Bereich der Übergreifung über Druckstreben in die vorhandene Bewehrung weitergeleitet. (Bild 2).

 
Bild 1: Tragwirkung eingemörtelter Bewehrungsstäbe ohne Anschlussbewehrung unter Zuglast (Verankerung)

Spieth, A. H.: Tragverhalten und Bemessung von eingemörtelten Bewehrungsstäben. Dissertation. Universität Stuttgart, 2002

 
Bild 2: Tragwirkung eingemörtelter Bewehrungsstäbe mit Anschlussbewehrung unter Zuglast (Übergreifungsstoß)

Spieth, A. H.: Tragverhalten und Bemessung von eingemörtelten Bewehrungsstäben. Dissertation. Universität Stuttgart, 2002

Um beim Bohren der Löcher für nachträglich eingemörtelte Bewehrungsstäbe eine Beschädigung des Betons zu vermeiden, wird in den Zulassungen eine relativ große, vom Bohrverfahren, der Bohrlochtiefe und dem Stabdurchmesser abhängige Betonüberdeckung gefordert. Zusätzlich hängt die Betondeckung davon ab, ob eine Bohrhilfe verwendet wird oder nicht.

Demgegenüber wurde die Betonüberdeckung der vorhandenen Bewehrung im bestehenden Bauteil abhängig vom angestrebten Korrosionswiderstand nach Stahlbetonregeln festgelegt und ist üblicherweise kleiner als die in den Zulassungen geforderte Überdeckung der nachträglich eingemörtelten Bewehrung. Um trotzdem Spalten des Betons zu verhindern, ist die Verankerungslänge nach Stahlbetonregeln deutlich größer und der Bemessungswert der Verbundspannungen fbd kleiner als nach Dübeltheorie. Durch Versuche wurde nachgewiesen, dass sich nachträglich eingemörtelte Bewehrungsstäbe bei Verwendung leistungsfähiger zugelassener Injektionsmörtel wie einbetonierte Stäbe verhalten. Deshalb dürfen für nachträglich eingemörtelte und einbetonierte Stäbe dieselben Bemessungswerte der Verbundspannungen angesetzt werden.

Die Bemessungswerte der Verbundspannungen sind in der jeweiligen ETA angegeben. Sie sind für die überwiegende Anzahl der zugelassenen Injektionssysteme identisch. Da sie jedoch systemabhängig sind, können in Einzelfällen – insbesondere für große Stabdurchmesser – abweichende Werte gelten.

ACHTUNG:

Werden die höheren Verbundspannungen nach der Dübeltheorie mit der kleineren Betonüberdeckung nach Regeln des Stahlbetonbaus kombiniert, dann fällt die Tragfähigkeit der Verankerung deutlich ab.

Ein wesentlicher Grundsatz des Stahlbetonbaus besagt, dass Zugspannungen im Bauteil durch geeignete Bewehrung aufgenommen werden müssen. Diese Forderung erklärt auch die in den ETAs zugelassenen Anwendungsfälle. In der Mehrzahl wird nämlich im bestehenden Bauteil eine Anschlussbewehrung verlangt, welche die durch die eingemörtelte Bewehrung eingeleiteten Zuglasten weiterleitet (Übergreifungsstoß, siehe Abschnitt a)). Nur in wenigen begründbaren Fällen wird keine Anschlussbewehrung gefordert und es liegt eine reine Verankerung vor (siehe Abschnitt b)). Die Nummerierung der Anwendungsfälle in den folgenden Abschnitten a) und b) entspricht derjenigen von DesignFiX auf dem Karteireiter VERANKERUNGSGRUND.

a) Anwendungsfälle mit Anschlussbewehrung

b) Anwendungsfälle ohne Anschlussbewehrung

In den Anwendungsfällen 4, 6 und 7 (obere Bewehrung) wird keine Anschlussbewehrung gefordert. Das lässt sich wie folgt begründen:

Anwendungsfall 4 → Wand / Stütze – Fundament (nur Druckkraft zulässig):

Da nur Druckkräfte zulässig sind, sind im vorhandenen Bauteil keine Zugkräfte weiterzuleiten.

Anwendungsfall 6 → Gelenkige Endverankerung von Platten / Balken:

Es liegt ein gelenkiger Anschluss vor und es sind nur Querkräfte jedoch keine einwirkenden äußeren Zugkräfte bzw. Biegemomente erlaubt. Im Bereich gelenkiger Endauflager stützt sich die Zugkraft in der Bewehrung auf Grund der Querkraft VEd (Fachwerkmodell) auf eine schräg verlaufende Druckstrebe ab (Bild 3), die einen Betonausbruch verhindert.

Bild 3: Abstützung der Zugkraft in der unteren Bewehrung infolge der einwirkenden Querkraft VEd (Fachwerkmodell) auf eine schräg verlaufende Druckstrebe

Anwendungsfall 7 → Deckung der Zugkraftlinie (obere Bewehrung)

In diesem Anwendungsfall darf die obere Bewehrung über einer Innenstütze abgestuft und verankert werden. Das entspricht EN 1992-1-1, Bild 9.2 (Zugkraftdeckung) und erfordert ebenfalls keine Anschlussbewehrung.

Bild 4: Zugkraftdeckung nach EN 1992-1-1, Bild 9.2

Die Kräfte in den Bewehrungsstäben infolge der einwirkenden Normalkraft und des Biegemoments lassen sich nicht direkt, sondern nur iterativ bestimmen. Die Normalkraft wirkt im Querschnittsschwerpunkt des neuen Bauteils und das Biegemoment in der Fuge zwischen vorhandenem und neuem Bauteil angenommen. Zunächst werden die Stabkräfte der neuen, nachträglich eingemörtelten Bewehrung bestimmt. Bei gleicher rechter und linker Betonüberdeckung der Bewehrung im neuen Bauteil stimmen die Schwerpunkte von Bewehrung und Beton überein und es liegt einachsige Biegung vor. Sind beide Betonüberdeckungen jedoch unterschiedlich, dann weicht der Schwerpunkt der Bewehrung von dem des Betonquerschnitts ab und der Nachweis muss für schiefe Biegung geführt werden.

Im zweiten Schritt werden die Stabkräfte der neuen Bewehrung auf die Bestandsbewehrung im alten Bauteil verteilt. Stimmt die Anzahl der Stäbe im alten und neuen Bauteil überein, dann sind die Stabkräfte gleich. Liegen im vorhandenen Bauteil mehr bzw. weniger Stäbe als im neuen, dann sind die Stabkräfte im vorhandenen Bauteil kleiner bzw. größer als im neuen Bauteil.

Es sind folgende Gleichgewichtsbedingungen zu erfüllen:

Einachsige Biegung (clinks = crechts ):

▪Σ N = 0

▪Σ M = 0

Schiefe Biegung (clinks ≠ crechts ):  

▪Σ N = 0

▪Σ Mx = 0

▪Σ My = 0

Der E-Modul des Bewehrungsstahls wird mit Es = 210000 N/mm² angenommen und für den Beton werden die Werte nach EN 1992-1-1, Tabelle 3.1 angesetzt.

Einwirkende Querkräfte bewirken auf Grund des Fachwerkmodells zusätzliche Zugkräfte in der Längsbewehrung und zusätzliche Druckkräfte im Beton (siehe Bild 5).

Bild 5: Zusätzliche Zugkräfte ΔFs in der Bewehrung und zusätzliche Druckkräfte ΔFc im Beton infolge einer Querkraft (Fachwerkmodell)

Nach EN 1992-1-1, Gleichung (6.18) beträgt diese zusätzliche Zugkraft:

ΔFs = 0,5 ∙ VEd ∙ (cot θ – cot α)

DesignFiX setzt senkrecht zur Bauteilachse angeordnete Bügel voraus (α = 90°). Damit vereinfacht sich obige Gleichung wie folgt:

ΔFs = 0,5 ∙ VEd ∙ cot θ

Der Winkel θ der Druckstrebe kann auf dem Karteireiter PRODUKTE - BERECHNUNG eingegeben werden.

In welcher Bewehrungslage die zusätzliche Zugkraft wirkt, hängt von der Richtung der Querkraft ab:

▪Anwendungsfälle 1 (Platte – Platte / Balken – Balken mit Auflager), 6 (Gelenkige Endverankerung von Platten / Balken) und 7 (Deckung der Zugkraftlinie):
→ Die zusätzliche Zugkraft wirkt bei nach unten gerichteter Querkraft in der unteren und bei nach oben gerichteter Querkraft in der oberen Bewehrungslage

▪Anwendungsfälle 2 (Platte – Platte / Balken – Balken) und Anwendungsfall 5 (Wand / Stütze Verlängerung):
→ Die zusätzliche Zugkraft wird in beiden Bewehrungslagen angesetzt, da nicht bekannt ist, wo sich die Auflager befinden und in welche Richtung die Druckstreben geneigt sind

▪Anwendungsfall 3 (Wand / Stütze – Fundament, Übergreifung):
→ Die zusätzliche Zugkraft wirkt bei nach links gerichteter Querkraft in der vorderen und bei nach rechts gerichteter Querkraft in der hinteren Bewehrungslage

▪Anwendungsfall 4 (Wand / Stütze – Fundament, nur Druckkraft zulässig):
Es sind keine Querkräfte zulässig

Der Bemessungswert der Übergreifungslänge beträgt:

l0 = α1 ∙ α2 ∙ α3 ∙ α5 ∙ α6 ∙ lb,rqd ≥ l0,min

Im Folgenden werden die einzelnen Faktoren beschrieben:

Faktor α1:

Die nachträglich eingemörtelte Bewehrung kann nur aus geraden Stäben bestehen. Deshalb ist der Faktor für die eingemörtelte Bewehrung immer α1 = 1.
Demgegenüber kann die vorhandene Bewehrung sowohl gerade als auch gebogen sein (Bild 6).

Bild 6: Mögliche Endverankerungen der Bewehrung im vorhandenen Bauteil

Bild 7: Maßgebende Betonüberdeckung cd

Der Faktor α1 darf bei gebogenen Stäben nur dann zu 0,7 gesetzt werden, wenn der Stab zugbeansprucht und die maßgebende Betonüberdeckung (Bild 7) cd > 3 ∙ ds ist. Anderenfalls ist α1 = 1. Sie müssen lediglich auf dem Karteireiter Struktur eingeben, ob die Bestandsbewehrung gerade oder gebogen ist. DesignFiX prüft dann automatisch, ob eine Zugbeanspruchung vorliegt und ob die Bedingung für die maßgebende Betonüberdeckung eingehalten ist und setzt dann den Faktor α1 zu 0,7 bzw. 1,0.

Faktor α2 :

Der Faktor α2 hängt von der wirksamen Betonüberdeckung (Bild 7) ab. Ist diese Überdeckung größer als der Mindestwert, dann kann darf α2 < 1 gesetzt werden. Für zugbeanspruchte Stäbe gilt:

Für druckbeanspruchte Stäbe ist der Faktor immer α2 = 1. Wie beim Faktor α1 prüft DesignFiX auch beim Faktor α2, ob die Stäbe zug- oder druckbeansprucht sind, bestimmt die wirksame Betonüberdeckung cd für die alte und die neue Bewehrung und berechnet α2.

Faktor α3 :

Dieser Faktor wird in DesignFiX sowohl für die Bestandsbewehrung als auch für die nachträglich eingemörtelte neue Bewehrung zu α3 = 1 gesetzt.

Faktor α5 :

Wirkt im Bereich des Übergreifungsstoßes ein Querdruck p, dann beträgt der Faktor α5:

α5 = 1 – 0,04 ∙ p        mit p [N/mm²]
≥ 0,7

≤ 1,0

Der Querdruck wird auf dem Karteireiter PRODUKTE - BERECHNUNG eingegeben.

Faktor α6 :

Grundsätzlich werden immer 100 % der Bewehrung in der Fuge zwischen vorhandenem und neuem Bauteil gestoßen. Der Faktor beträgt deshalb immer α6 = 1,5.        

Grundwert der Verankerungslänge lb,rqd :

Der Grundwert der Verankerungslänge errechnet sich nach EN 1992-1-1, Gleichung (8.3):

lb,rqd = (Ø / 4) ∙ (σSd / fbd)

Die Stahlspannung σSd errechnet sich aus der Stabkraft und dem Querschnitt des Bewehrungsstabes. Der Bemessungswert der Verbundfestigkeit fbd der Bestandsbewehrung hängt von den Verbundbedingungen sowie der Betonfestigkeit ab. Die Verbundfestigkeit der neuen, nachträglich eingemörtelten Bewehrung wird in manchen Fällen zusätzlich vom Bohrverfahren und dem Stabdurchmesser beeinflusst.

Die Verbundbedingung hängt von der Lage der Bewehrung im Bauteil ab (Bild 8).

Bild 8: Verbundbedingungen nach EN 1992-1-1, Bild 8.2

Der Bemessungswert der Verbundfestigkeit fbd beträgt für die Bestandsbewehrung:

fbd = 2,25 ∙ η1 ∙ η2 ∙ fctd

Mit der 5%-Fraktile der charakteristischen zentrischen Betonzugfestigkeit nach EN 1992-1-1, Tabelle 3.1 und einem Teilsicherheitsbeiwert γc = 1,5 erhält man für Stabdurchmesser Ø ≤ 32 mm folgende Bemessungswerte der Verbundfestigkeit:

Tabelle 1: Bemessungswerte der Verbundfestigkeit einbetonierter Bewehrungsstäbe Ø ≤ 32 mm nach EN 1992-1-1

Die Bemessungswerte der Verbundfestigkeit fbd für die nachträglich eingemörtelte Bewehrung sind in Abhängigkeit von der Betonfestigkeit, den Verbundbedingungen und ggf. vom Bohrverfahren und dem Stabdurchmesser in der jeweiligen ETA angegeben.

Mindestwert der Übergreifungslänge l0,min :

Die minimale Übergreifungslänge beträgt nach EN 1992-1-1, Abschnitt 8.7.3:

Einfluss des lichten Abstandes zwischen vorhandener und neuer Bewehrung auf den Bemessungswert der Übergreifungslänge:

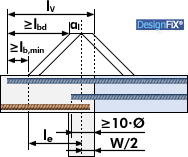
Der berechnete Bemessungswert l0 der Übergreifungslänge setzt voraus, dass der lichte Abstand der Stäbe der vorhandenen und neuen eingemörtelten Bewehrung das Vierfache des Stabdurchmessers nicht überschreitet. Nur so sind die Druckstreben zwischen vorhandenen und neuen, eingemörtelter Bewehrungsstäben voll wirksam (Bild 2). Ist der lichte Abstand der Stäbe größer, dann ist die rechnerischer Übergreifungslänge um die Differenz zwischen dem vorhandenen lichten Stababstand und 4 ∙ Ø zu vergrößern. Bild 9 zeigt ein Beispiel und Bild 10 die detaillierte Vermaßung der Bewehrungsstäbe.

Bild 9: Beispiel mit unterschiedlicher Lage der vorhandenen und der neuen, eingemörtelten Bewehrung

Bild 10: Vermaßung der Achsabstände der Bewehrungsstäbe (Beispiel Bild 9)

Der größte lichte Abstand zwischen den alten und neuen Stäben (rote Doppelpfeile in Bild 18) beträgt: mm.
Damit beträgt der Zuschlag Bemessungswert l0 der Übergreifungslänge: l0,e = 68,1 – 4 ∙ 10 = 28,1 mm.

Der Bemessungswert der Verankerungslänge beträgt:

lbd = α1 ∙ α2 ∙ α3 ∙ α4 ∙ α5 ∙ lb,rqd ≥ lb,min

Faktoren α1, α2, α3, α5 und Grundwert der Verankerungslänge lb,rqd  siehe Abschnitt „Bestimmung der Übergreifungslänge nach EN 1992-1-1, Abschnitt 8.7.3“.

Der Faktor α4 wird grundsätzlich zu α4 = 1 gesetzt.

Die Mindestwert der Verankerungslänge lb,min beträgt:

Zugbelastete Bewehrungsstäbe

lb,min = max {0,3 ∙ lb,rqd,fyd; 10 ∙ Ø; 100 mm}

Druckbelastete Bewehrungsstäbe

lb,min = max {0,6 ∙ lb,rqd,fyd; 10 ∙ Ø; 100 mm}